アルベルト・アインシュタイン
皆さんご存知ですか?
一般相対性理論を提唱した物理学者で有名です。
(僕は物理学に関しては、まったくわかりません。笑)
天才物理学者のアインシュタイン
その彼が「人類最大の発明」と呼んだのは、意外にも”資産運用にまつわる概念”でした。
複利効果とは、資産運用においての基礎の基礎というべき概念です。
おそらく高校生の授業でも、必ず教える事になると思います。
しかし複利効果に関して、資産形成を初めて勉強する方は、ご存じない方もいらっしゃると思います。
そこで今回の記事では、
・複利効果とはどういうものなのか?
・複利効果を使った、便利な投資の法則
について、紹介していきます。
将来に向けた資産形成において、非常に大切な考え方です。
10代、20代の方はもちろん、老後の資金準備を考えている方も、是非参考にして下さい。
複利効果=ゆきだるま!?
複利効果を一言で表すと、複利効果は雪だるまです!
雪だるまといっても、出来上がった可愛い雪だるまではなく、
雪の球をコロコロ転がしている最中を思い浮かべてください。
雪の上をコロコロ転がすと、どんどん大きくなっていきますよね?
雪の球の上に雪が重なって、一回り大きくなった雪の球の上にまた雪が重なって…
これが繰り返されて、雪玉が大きくなっていきます。

これを資産運用に落とし込むと・・・
[“単利”という複利ではない制度]
1年目は、110万円。
2年目は、120万円。
3年目は、130万円になります。
[100万円を年10%の利率で3年”複利で”運用]
1年目は、110万円。
2年目は、121万円。
3年目は、133万1,000円になります。
比べると、複利運用の方が増えていますね。
中身を詳細に説明すると
単利は100万円に対して毎年10%が利子でついています。
1年目に100万円に10%の利率がつき110万円、2年目には100万円に10%の利率がつき110万円に昨年の10万円がプラスされ120万円、3年目には100万円に10%が付き110万円に1年目の10万円、2年目の10万円の合計20万円がプラスされ130万円になるのが単利です。
それに対し複利は
1年目に100万円に10%の利率がつき110万円、2年目には110万円に10%の利率がつき121万円、3年目には121万円に10%が付き133万1,000円になるのが複利です。
[図解]
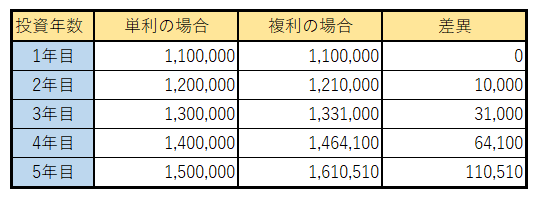
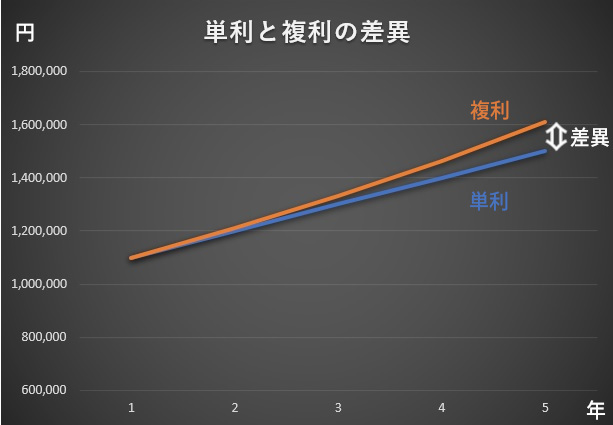
このように複利運用は年数が重なれば重なるほど、大きく成長していくという事になります。
複利と単利の違いは、毎年増える利率に応じて増えるお金(ここでは1万円)が
・元本にプラスされて雪だるまのように増えていく(複利)
・元本にプラスされず、払い出されていく(単利)
という部分です。
資産を2倍にする複利の計算「72の法則」
複利運用において、何年間で資金を2倍にしたいか希望年数を決め、その為には何%の金利が必要なのかを計算で求める事が出来ます。
計算式は、72÷利率=2倍になる年数
それを72の法則と呼びます。
この法則は分かりやすく簡単なので、授業で教える事になるのでしょう!
例を挙げて早速計算してみます。
前回の[親からは「貯金をしなさい」と教えられてしまう訳]の記事で活用した計算方法です。
・現在の銀行の定期金利0.002%を72の法則で複利運用とした場合
72÷0.002=36000
36000年かかるようです。
もはや、人類が地球にいるのか定かではありません。
・1990年代初め、銀行の金利が約7%程度ついていた時
72÷7=10.29(小数点第三位以下切り上げ)
7%だと約10年です。
上の計算例とはえらい違いですね。笑
単利の計算「100の法則」
単利運用でも同じように、何年間で資金を倍にしたいか希望年数を決め、その為には何%の金利が必要なのかを計算で求める事が出来ます。
単利運用の場合は、100の法則と呼びます。
計算式は、100÷利率=2倍になる年数
3倍複利「115の法則」
「2倍なんかじゃ足らない…3倍返しだッッ!!」
なんて方は、複利で3倍にする期間も計算できます。笑
こちらも計算方法は同じで
115÷利率=3倍になる年数
まとめ:複利効果は人類最大の発明であり、資産運用の基礎
今回の記事では、
・複利効果とはどういうものなのか?
・複利効果を使った、便利な投資の法則
について解説しました。
アインシュタインが人類最大の発明と呼んだ、「複利効果」
複利効果は雪だるまのように増えていく。
72の法則をはじめとした便利な計算方法がある。
この2点は是非覚えておきましょう!
複利は資産運用の基礎であり、効率よく上手に行う際のキーワードになってきます。
例題で計算をしましが、結果を見ると複利効果を使えば、かなり資産の成長スピードも速くなっていきます。
裏を返すと、若いうちから資産運用をしておくor勉強しておくことは、運用期間が長いという武器を手に入れられるわけです!
若ければ若いほど有利…
高校生で教えてもらえるなんて、非常にありがたい話なんですね。
金融機関で運用の話を進められた時なども、72の法則は使えます!
是非参考にしてみてください。



コメント